Landau–Lifshitz–Gilbert equation
In physics, the Landau-Lifshitz-Gilbert equation , named for Lev Landau and Evgeny Lifshitz and T. L. Gilbert, is a name used for a differential equation describing the precessional motion of magnetization M in a solid. It is a modification by Gilbert of the original equation of Landau and Lifshitz.
The various forms of the equation are commonly used in micromagnetics to model the effects of a magnetic field on ferromagnetic materials. In particular it can be used to model the behaviour of hard disk drives [1].
Contents |
Landau-Lifshitz ordinary differential equation
The LL equation was introduced by Landau & Lifshitz (1935) to model the precessional motion of magnetization  in a solid with an effective magnetic field
in a solid with an effective magnetic field 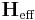 and with damping. It is the ordinary differential equation[2][3][4]
and with damping. It is the ordinary differential equation[2][3][4]
The constant  is the Landau-Lifshitz phenomenological damping parameter and depends on the solid, and
is the Landau-Lifshitz phenomenological damping parameter and depends on the solid, and  is the electron gyromagnetic ratio.
is the electron gyromagnetic ratio.
Using the methods of irreversible thermodynamics, numerous authors have independently obtained the Landau-Lifshitz equation. [5]
In irreversible thermodynamics, the thermodynamic forces are non-zero when the system is out of equilibrium. Here the thermodynamic force is the cross-product  ; hence only the vectors
; hence only the vectors  (precession) and
(precession) and 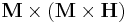 (damping) are allowed in
(damping) are allowed in 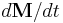 . The result is the Landau-Lifshitz form.
. The result is the Landau-Lifshitz form.
Landau-Lifshitz-Gilbert equation
In 1955 Gilbert replaced the damping term, by introducing some kind of viscous force. This led to the following, obviously even more complicating expression, known as the Landau-Lifshitz-Gilbert equation (LLG-E):
Surprisingly this can be transformed by a somewhat cumbersome calculation [6] into an equivalent expression where the additional complications seem to have been transformed away,
Here we have used the identification 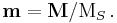 Now the final summand, containing the damping, looks simpler.
Now the final summand, containing the damping, looks simpler.
The LL-E above, (1), works fairly well when the damping is small, but fails for large damping (α comparable to or greater than unity). This problem was fixed by Gilbert through his modification, (2a), or equivalently (2b)[7].
References and footnotes
- ^ Yang, Bo. "Numerical Studies of Dynamical Micromagnetics". http://physics.ucsd.edu/~drf/pub/bo-thesis.ps.gz. Retrieved 8 August 2011.
- ^ Aharoni 1996
- ^ Brown 1978
- ^ Chikazumi 1997
- ^ [See T. Iwata, J. Magn. Magn. Mater. 31–34, 1013 (1983); T. Iwata, J. Magn. Magn. Mater. 59, 215 (1986); V.G. Baryakhtar, Zh. Eksp. Teor. Fiz. 87, 1501 (1984); S. Barta (unpublished, 1999); W. M. Saslow, J. Appl. Phys. 105, 07D315 (2009).]
- ^ The essential step is, to exploit the identity
![... %2B\alpha^2\,\textbf m\times [\textbf m\times (d/dt)\textbf m]\equiv ... -\alpha^2\,(d/dt)\textbf m\,.](/2012-wikipedia_en_all_nopic_01_2012/I/ed7d22ea62e561c5e58737ea7f6b468c.png)
- ^ For details of Kelly's non-resonant experiment, and of Gilbert's analysis (which led to Gilbert's modifying the damping term), see T. L. Gilbert and J. M. Kelly, "Anomalous rotational damping in ferromagnetic sheets", Conf. Magnetism and Magnetic Materials, Pittsburgh, PA, June 14–16, 1955 (New York: American Institute of Electrical Engineers, Oct. 1955, pp. 253-263). Text references to Figures 5 and 6 should have been to Tables 1 and 2. Gilbert could not fit Kelly's experiments with fixed usual gyromagnetic ratio γ and a frequency-dependent λ=αγ, but could fit that data for a fixed Gilbert gyromagnetic ratio γG
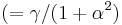 and a frequency-dependent α. Values of α as large as 9 were required, indicating very broad absorption, and thus a relatively low-quality sample. Modern samples, when analyzed from resonance absorption, give α's on the order of 0.05 or less.
and a frequency-dependent α. Values of α as large as 9 were required, indicating very broad absorption, and thus a relatively low-quality sample. Modern samples, when analyzed from resonance absorption, give α's on the order of 0.05 or less.
See also
External links
Literature
- Aharoni, Amikam (1996). Introduction to the Theory of Ferromagnetism. Clarendon Press. ISBN 0198517912. http://www.oup.com/us/catalog/general/subject/Physics/ElectricityMagnetism/?view=usa&ci=9780198508090.
- Brown, Jr., William Fuller (1978) [Originally published in 1963]. Micromagnetics. Robert E. Krieger Publishing Co.. ISBN 0-88275-665-6.
- Chikazumi, Sōshin (1997). Physics of Ferromagnetism. Clarendon Press. ISBN 0-19-851776-9.
- Gilbert, T.L. (1955), "A Lagrangian formulation of the gyromagnetic equation of the magnetic field", Physical Review 100: 1243. This is only an abstract; the full report is "Armor Research Foundation Project No. A059, Supplementary Report, May 1, 1956", but was never published. A description of the work is given in Gilbert, T. L. (2004), "A phenomenological theory of damping in ferromagnetic materials", IEEE Trans. Mag. 40 (6): 3443–3449, Bibcode 2004ITM....40.3443G, doi:10.1109/TMAG.2004.836740
- Landau, L.D.; Lifshitz, E.M. (1935), "Theory of the dispersion of magnetic permeability in ferromagnetic bodies", Phys. Z. Sowietunion 8, 153
- Skrotskiĭ, G V (1984), "The Landau-Lifshitz equation revisited", Sov. Phys. Usp. 27 (12): 977–979, Bibcode 1984SvPhU..27..977S, doi:10.1070/PU1984v027n12ABEH004101
- Guo, Boling; Ding, Shijin (2008), Landau-Lifshitz Equations, Frontiers of Research With the Chinese Academy of Sciences, World Scientific Publishing Company, ISBN 978-9812778758